Abstract
This article compares and contrasts the ability of three machine-learning algorithms to discover a rectangular decision boundary in a supervised classification exercise; Support Vector Machines, Multivariate Logistic Regression with Causal Factors, and Recursive Trees are benchmarked against a hypothetical dataset of rectangular 2-Dimensional geometry.
Discussion
This article extends a previous article on the analytical construction of a curvilinear classification decision boundary using Multivariate Logistic Regression. During a recent constructive LinkedIn discussion regarding the utility of Recursive Trees and high-dimensional stochastic simulation with Trees, commonly termed “Random Forests,” it was observed that Trees and Forests can find a non-linear decision boundary with which to classify a class. One correspondent observed that this dexterity comes at the expense of multiple adjustable parameters and hyperparameters such that, notwithstanding the purported “interpretability” of Trees and Forests, these powerful classification algorithms returned very little domain knowledge of the problem set’s data-generating function; better to curate the Features of the Analytic Data Set (ADS) and submit the ADS to Regression analysis, which returns coupling constants and the standard error of the central tendency of those constants, which when considered in tandem, hint at the Multiphysics of the problem set.
The discussion then conjectured that classifying two classes that were separated by a hypothetical rectangular decision boundary would be difficult by regression but straight-forward by trees or forests.
All parties agreed with that conjecture’s intuition.
This article simply documents this experiment and returns it to the LinkedIn conversation for further consideration and discussion.
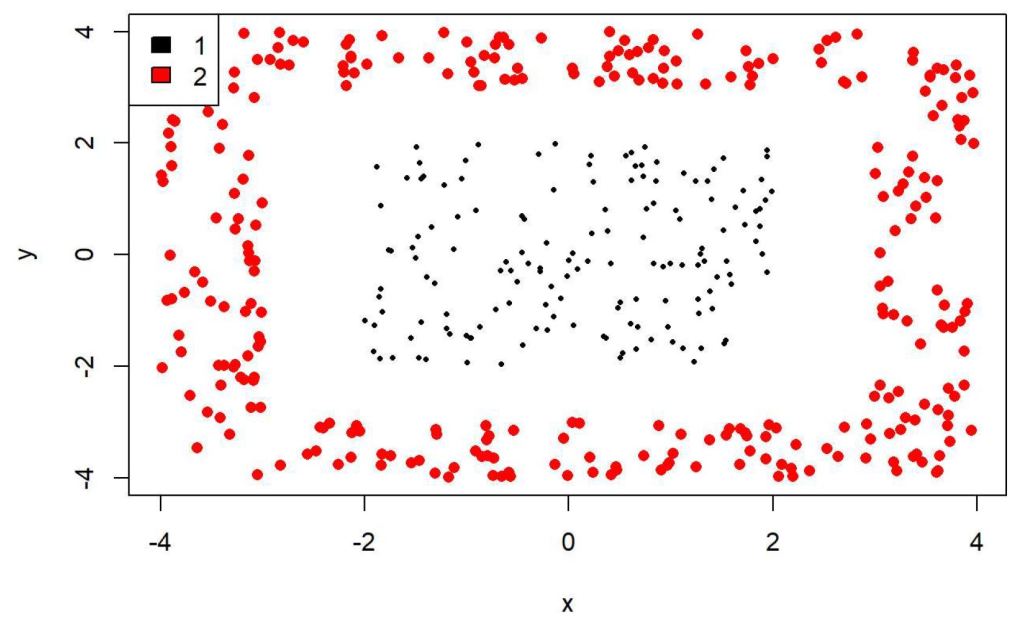
Let’s get started.
DOWNLOAD THE PAPER BELOW TO CONTINUE READING…